Econ101: Supply and Demand
Econ101 presents a set of foundational notions about prices and markets, namely the supply and demand framework, which makes a lot of assumptions, some of them hard to justify. This leads to an intellectually fragile specialized analytical framework that does not allow for general or abstract thinking. While it is useful to think about pricing and bidding processes in the context of opposing interests of buyers and sellers, supply and demand should be considered an emergent phenomenon, and not a foundational one. Supply and demand emerges after property, markets, government, and infrastructure are established.
The conditions leading to smooth and opposing price curves are complex, and supply and demand does not equip one to think very basically about how these opposing price curves emerge.
Meanwhile, in a typical second year computer science course, a comparable topic on resource management is covered, and that is the limiting resource costs of algorithms. "Big Oh" notation is the broad brush technique computer scientists use to measure what algorithms will cost.
Computer Science 202: Big Oh Notation
The big "oh" notation used in computer science is what is called "asymptotic analysis" in mathematics. It is used to characterize the performance or resource costs of an algorithm, a formal repeatable process, as the size of the input increases. The resource cost is often the running time of the algorithm, but it could also be something else like memory utilization.
For example, computer science students learn various algorithms how to sort lists of numbers. Under typical assumptions, the longer the list of numbers, the longer it will take to sort them. But there is not just one process that will sort a list. Imagine you had a deck of playing cards numbered 1 through 52. How would you go about sorting them?
One could split the deck in half and sort each half deck of 26 cards. But how do you sort the half a deck? Well, you can simply split that half deck into quarter decks. Eventually you get to a situation where you have 2 or 3 cards. Once you have 2 "subdecks" sorted, you can combine them by having the two decks face up and pulling the lowest or highest card to put in a third deck face down, depending on the way you are sorting. This "algorithm" is known as merge sort. It can be performed just as easily with a computer as it can by hand. You could even record people doing these algorithms by hand.
Merge sort has a "big oh" runtime cost of N log N. As the size of the deck increases, given by N, you must traverse a list of length N a number of times,
The exact runtime cost in the case of 52 cards is the following:
- Split the deck into two 26 card stacks (count 26 cards)
- Split those stacks into 4x 13 card stacks (count 13 cards twice)
- Split those decks into 4x 7 card stacks and 4x 6 card stacks (count 6 cards four times)
- Split those decks into 4x 4 card stacks 12x 3 card stacks (count 8*3 cards)
- Split the 4 card stacks into 8x 2 card stacks. (count 8*2 cards)
- Sort all the 2 and 3 card stacks (3 comparisons * 12 stacks + 1 comparison * 8 stacks)
- Merge stacks in the same way you split them (about 52 comparisons per level * 6 merge levels)
This leads to a total of 26 + 2*13 + 4*6 + 8*3 + 8*2 = 116 counts, and about 312 comparisons.
Note, to save space, you only need to split and merge one half of the deck at a time, you can set aside one half deck while you split the other, and the same on each recursive level.
But what if we had N = 5,000 cards, or N = 5 million cards? How long would our merge sort take then?
The number of recursive levels for the split/merge process is going to be the base 2 log of the total number of cards. We have to count out about half the cards at each level, and we have to make comparisons approximately equal to the total number of cards at each level.
Imagine that it takes 0.3 seconds to count a card, and it takes 1 full second to compare two cards. Then the number of seconds it takes to perform a merge sort with a deck of cards, is approximately:
Briefly, what big oh notation does, is remove all constant factors, and simply look at the shape of the curve. Because performance can vary so drastically for large inputs, the shape of the curve becomes much more important than these constant factors. We know a N^2 algorithm will eventually run a lot slower than an N log N algorithm, once N gets big enough.
Comparison
Both these classes use curves to measure resource costs. But in the computer science case, students have enough experience to understand that these curves don't just come out of the ether. They are the result of a formal, repeatable process, which we simplify down into a simplified description. The resource analysis in the computer science case is much more rigorous in terms of scale. Specifically, computer science students understand how and why "constant returns to scale", does not apply to most algorithms and resource problems.
In general, computer science and economics cover much of the same problem, that of efficiently allocating resources to solve problems. But I find the analytical framework developed by computer science to be much more general and adaptable, which I believe makes it better suited for understanding economics as well, once someone has gained more experience with mathematical optimization and an understanding of logistics and operations.
Prices both communicate underlying costs, but they also negotiate the allocation of what economists call "surplus". This is important, and the ability to think about economic problems in generalized terms means that one can distinguish between these two dual functions of prices.
This is not to say, that no economists understand the nuances of real resource problems, or that engineers and computer scientists could wholesale replace economists without more formal training. But being a skilled engineer involves a lot of time and experience with specific problem solving, debugging and optimizing. In a sense, it is much more difficult for economists to get this kind of practical experience, and they are often forced to rely on mathematical formalisms and statistical techniques over repetition and experimentation.
That being said, there is a lot more cross disciplinary work being done than ever. But I think that the insights of computer science and other engineering-like disciplines to economists can be more about the history of economic development, specifically, the history of post-keynesian economics. For a long time, post-keynesian economics was disregarded because it often lacked the same mathematical formalisms, specifically because post-keynesians rejected what they considered to be overly simplistic models based on not merely simplifying or approximating assumptions, but fantastical and greatly misleading ones.
There are many cases in finance and economics where mathematical formalism is important and completely practical, for example, in terms of accounting identities, and measuring stocks and flows of both real and financial resources. But much of the mathematical formalism that seeks to link economic variables in a causal fashion has proven to be either severely limited or hopelessly naive and unrealistic. Sometimes, the lack of ambitious equations and specific causal quantitative relationships is the most realistic and practical approach.
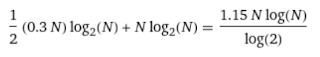


Comments
Post a Comment